如果你去看一篇实证研究的学术论文,特别是金融、投资等相关领域的论文,你会发现, 在这些实证论文的结果大多以图和表的形式展示。常见的结果表格类型包括:描述性统计表格、相关系数表格(出现的频率下降了)、单变量分析表格、回归分析表格(多个)。
本章首先介绍描述性统计结果生成、相关系数的计算和结果如何导出到Excel表格、Word表格。 随后本文将介绍一元和多元OLS回归分析的命令、回归结果的解读以及如何快速生成符合论文要求的回归结果,随后本章会结合多元OLS介绍对系数的假设检验,最后本章介绍更多的回归模型命令和常见的处理方法。
描述性统计与相关性分析
描述性统计 tabstat
在实证分析论文中,通常都需要给出论文中涉及变量的描述性统计表格,描述新统计是指各个变量的统计量,包括:样本量、最小值、最大值、中位数、25分位数、 75分位数、偏度、峰度等。 使用到的命令是tabstat得到想要的结果。通过help tabstat查看该命令的帮助文档。
以系统自带数据文件auto.dta为例,如果我们要生成变量price, mpg, turn等三个变量的描述性统计,首先通过如下命令在结果窗口(Result Window)中得到相关的结果:
sysuse auto, clear // column(statistics)选项是把统计量作为列(默认是将统计量作为行、变量作为列展示) // statistics(...)选项指定了要报告哪些统计量 tabstat price mpg turn, columns (statistics ) /// statistics (N mean sd min p25 p50 p75 p95 max )
. sysuse auto, clear
(1978 automobile data)
. // column(statistics)选项是把统计量作为列(默认是将统计量作为行、变量作为列展
> 示)
. // statistics(...)选项指定了要报告哪些统计量
. tabstat price mpg turn, columns(statistics) ///
> statistics(N mean sd min p25 p50 p75 p95 max)
Variable | N Mean SD Min p25 p50
-------------+------------------------------------------------------------
price | 74 6165.257 2949.496 3291 4195 5006.5
mpg | 74 21.2973 5.785503 12 18 20
turn | 74 39.64865 4.399354 31 36 40
--------------------------------------------------------------------------
Variable | p75 p95 Max
-------------+------------------------------
price | 6342 13466 15906
mpg | 25 34 41
turn | 43 46 51
--------------------------------------------
.
相关系数矩阵 corr (pwcorr)
相关系数反映了两个变量之间相互变动的关联性,定义为:
r=\frac{\sum{{X-\bar{X})(Y-\bar{Y})}}}{\sqrt{\sum{(X-\bar{X})^2}\sum{(Y-\bar{Y})^2}}}
与相关系数相关的一个概念是协方差,定义为
r=\sum{{X-\bar{X})(Y-\bar{Y})}}
可以看出,二者都代表两个变量X和Y之间的相关性大小,只是相关系数使用X和Y的标准差进行了标准化处理(使得不同情况下的相关系数具有可比性)。
在Stata与计算相关系数和协方差的有关的命令是correlate和pwcorr。可以通过 hlep correlate 命令获取它们的帮助文档。
仍然以系统自带数据auto.dta为例,假设我们要得到 price mpg turn三个变量的相关系数(矩阵)可以首先通过如下命令将相关系数输出到结果窗口
sysuse auto, clear corr price mpg turn rep78pwcorr price mpg turn rep78
. sysuse auto, clear
(1978 automobile data)
. corr price mpg turn rep78
(obs=69)
| price mpg turn rep78
-------------+------------------------------------
price | 1.0000
mpg | -0.4559 1.0000
turn | 0.3302 -0.7355 1.0000
rep78 | 0.0066 0.4023 -0.4961 1.0000
. pwcorr price mpg turn rep78
| price mpg turn rep78
-------------+------------------------------------
price | 1.0000
mpg | -0.4686 1.0000
turn | 0.3096 -0.7192 1.0000
rep78 | 0.0066 0.4023 -0.4961 1.0000
.
corr命令与pwcorr命令的区别在于,当变量中存在缺失值时,corr计算相关系数仅基于所有变量都不存在缺失值的观测值(行)进行计算,而pwcorr则只需要每一组计算相关系数的变量的取值都不是missing即可。
随后可以利用描述性统计中类似的方法,将结果拷贝到Excel表格和Word表格。当然也可以利用logout命令。
单变量分析
t检验
t检验可以用于检验某个变量的均值是否等于某个常数、或者两个变量的均值是否相等。可以分为单个总体的假设检验和两个总体的假设检验和配对t检验。在Stata中,我们主要使用命令ttest进行t检验。
单个总体下的t检验
这类t检验是在方差未知的情况下,检验变量均值是否等于某个常数。
sysuse auto, clear summarize mpg ttest mpg == 20
. sysuse auto, clear
(1978 automobile data)
. summarize mpg
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
mpg | 74 21.2973 5.785503 12 41
. ttest mpg == 20
One-sample t test
------------------------------------------------------------------------------
Variable | Obs Mean Std. err. Std. dev. [95% conf. interval]
---------+--------------------------------------------------------------------
mpg | 74 21.2973 .6725511 5.785503 19.9569 22.63769
------------------------------------------------------------------------------
mean = mean(mpg) t = 1.9289
H0: mean = 20 Degrees of freedom = 73
Ha: mean < 20 Ha: mean != 20 Ha: mean > 20
Pr(T < t) = 0.9712 Pr(|T| > |t|) = 0.0576 Pr(T > t) = 0.0288
.
可以看到,该t-检验对应的t-统计量为1.9289,对应的双侧t-检验p值为0.0576,表明显著性水平接近5.8%。
两个总体下的t检验
这类t检验是在方差未知的情况下,检验两个变量的均值是否相等。 在下面的例子中,我们要检验的数据在一个变量中(mpg),通过另一个变量(treated)的取值来指示t检验对应的两个样本,也就是treated=1和treated=0两种。
sysuse auto, clear tab foreign, missing tabstat mpg, by (foreign) s (N mean sd min max )ttest mpg, by (foreign)
. sysuse auto, clear
(1978 automobile data)
. tab foreign, missing
Car origin | Freq. Percent Cum.
------------+-----------------------------------
Domestic | 52 70.27 70.27
Foreign | 22 29.73 100.00
------------+-----------------------------------
Total | 74 100.00
. tabstat mpg, by(foreign) s(N mean sd min max)
Summary for variables: mpg
Group variable: foreign (Car origin)
foreign | N Mean SD Min Max
---------+--------------------------------------------------
Domestic | 52 19.82692 4.743297 12 34
Foreign | 22 24.77273 6.611187 14 41
---------+--------------------------------------------------
Total | 74 21.2973 5.785503 12 41
------------------------------------------------------------
. ttest mpg, by(foreign)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Group | Obs Mean Std. err. Std. dev. [95% conf. interval]
---------+--------------------------------------------------------------------
Domestic | 52 19.82692 .657777 4.743297 18.50638 21.14747
Foreign | 22 24.77273 1.40951 6.611187 21.84149 27.70396
---------+--------------------------------------------------------------------
Combined | 74 21.2973 .6725511 5.785503 19.9569 22.63769
---------+--------------------------------------------------------------------
diff | -4.945804 1.362162 -7.661225 -2.230384
------------------------------------------------------------------------------
diff = mean(Domestic) - mean(Foreign) t = -3.6308
H0: diff = 0 Degrees of freedom = 72
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0003 Pr(|T| > |t|) = 0.0005 Pr(T > t) = 0.9997
.
We do not find a statistically significant difference in the means.
待检验的两组数据也可以用不同的变量来表示,例子如下:
webuse fuel, clear describe ttest mpg1==mpg2也许你注意到了,两个例子的t检验结果是不一样的,尽管这两个数据本质上是一样的(请观察两个数据,并尝试实现数据fuel.dta和full3.dta的相互转化)。这是因为二者的计算逻辑不同,第二个例子中本质上是用的配对t检验 ,换句话说,在第二个例子中,我们首先计算每一个数据行对应的(mpg1, mpg2)取值的差值,然后基于差值构造t统计量。而在第一个例子中,我们是分别计算treated==1和treated==2的这两个字样本中mpg的均值和标准,并构造t统计量。你可以从两个结果中关于diff即变量的差值的计算方式上看出来,在第一个例子中mean(diff)=mean(0)-mean(1),而第二个例子中,mean(diff)=mean(mpg1-mpg2)。
OLS回归分析
OLS回归原理
(这部分推导请阅读计量经济学相关教材内容,例如伍德里奇《计量经济学导论现代观点》Introiductory Econometrics A Modern Approach)
OLS是ordinary least square的简称,意为“普通最小二乘法”。OLS的估计建立在如下线性回归模型的基础上:
y_{i,t}=\beta_0 +\beta_1 x_{1,t} + \beta_2 x_{2,t} + \cdots + \beta_k x_{k,t} + \varepsilon
其中 y 是因变量 x_1 至 x_k 是 k 个自变量。我们可以把上述方程改写为向量的形式:
\mathbf{y}=\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\varepsilon}
这里向量 \mathbf{y} 是 (y_1, y_2, \cdots, y_n)^T 共计 n 个元素的列向量;n \times (1+k) 维矩阵 \mathbf{X} 中的第一列是全1的向量,是回归中的自变量; 向量 \boldsymbol{\beta} 是指 (\beta_0, \beta_1, \beta_2, \cdots, \beta_k)' 共计 k+1 个元素的向量,是需要估计的参数; 向量 \boldsymbol{\varepsilon}=(\varepsilon_1, \varepsilon_2, \cdots, \varepsilon_n)' ,代表扰动项。
OLS回归估计参数的 \boldsymbol{\beta} 的思想是最小化残差平方和,即 \min \mathbf{e}^T\mathbf{e} = \min \sum_{i=1}^n{e_i^2} ,从根据最小化问题的一阶条件推导出待估参数的最小二乘估计表达式:
\hat{\boldsymbol{\beta}}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}
当 \mathbf{X} 中只有一个元素也就是当自变量只有一个的时候,对应的方程可以写成 y=\beta_0 +\beta_1 x +\varepsilon ,待估计的参数有两个 \beta_0 和 \beta_1 。
这里得到的估计系数 \hat{\beta}_1 代表了根据样本数据估计得到的变量 x 对变量 y 的边际影响—— x 增加一个单位,y 对应增加 \hat{\beta}_1 个单位。
OLS回归Stata命令
在Stata中,OLS估计结果使用命令regress得到,通过help regress可以查看该命令的帮助文档。
regress命令的基本语法结构为:
regress depvar [indepvars] [if ] [in ] [weight ] [,options]其中,regress是命令名称,depvar是指回归中的因变量;indepvars代表(多个)自变量名称列表;if代表条件语句,in代表范围语句,weight代表权重语句,options代表其他选项。
常用的options包括:
noconstant
模型不包含常数项
level(#)
设定置信区间
beta
数据标准化下的回归系数
vce(type)
设置标准误的类型,除了默认的ols外,常用的还有robust, cluster bootstrap, hs2, hc3等
接下来,我们基于系统自带数据auto.dta,首先考察weight和length两个变量对mpg变量的影响,回归模型设定如下:
mpg = \beta_0 + \beta_1 weight +\beta_2 length
sysuse auto, clear regress mpg weight reg mpg length reg mpg weight length
. sysuse auto, clear
(1978 automobile data)
. regress mpg weight
Source | SS df MS Number of obs = 74
-------------+---------------------------------- F(1, 72) = 134.62
Model | 1591.9902 1 1591.9902 Prob > F = 0.0000
Residual | 851.469256 72 11.8259619 R-squared = 0.6515
-------------+---------------------------------- Adj R-squared = 0.6467
Total | 2443.45946 73 33.4720474 Root MSE = 3.4389
------------------------------------------------------------------------------
mpg | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
weight | -.0060087 .0005179 -11.60 0.000 -.0070411 -.0049763
_cons | 39.44028 1.614003 24.44 0.000 36.22283 42.65774
------------------------------------------------------------------------------
. reg mpg length
Source | SS df MS Number of obs = 74
-------------+---------------------------------- F(1, 72) = 124.33
Model | 1547.35715 1 1547.35715 Prob > F = 0.0000
Residual | 896.102311 72 12.4458654 R-squared = 0.6333
-------------+---------------------------------- Adj R-squared = 0.6282
Total | 2443.45946 73 33.4720474 Root MSE = 3.5279
------------------------------------------------------------------------------
mpg | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
length | -.2067688 .018544 -11.15 0.000 -.2437355 -.1698021
_cons | 60.15586 3.509057 17.14 0.000 53.16068 67.15104
------------------------------------------------------------------------------
. reg mpg weight length
Source | SS df MS Number of obs = 74
-------------+---------------------------------- F(2, 71) = 69.34
Model | 1616.08062 2 808.040312 Prob > F = 0.0000
Residual | 827.378835 71 11.653223 R-squared = 0.6614
-------------+---------------------------------- Adj R-squared = 0.6519
Total | 2443.45946 73 33.4720474 Root MSE = 3.4137
------------------------------------------------------------------------------
mpg | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
weight | -.0038515 .001586 -2.43 0.018 -.0070138 -.0006891
length | -.0795935 .0553577 -1.44 0.155 -.1899736 .0307867
_cons | 47.88487 6.08787 7.87 0.000 35.746 60.02374
------------------------------------------------------------------------------
.
在这里,我们先分别单独考察了weight和length对mpg的影响,第三个模型将mpg和weight都作为自变量加入模型,同时考察两个变量对price的影响。
regress命令的回归结果可以分为上下两个部分,上半部分主要是回归模型整体的统计量,其中左边是方差分析(ANOVA)的结果,包括:
SS是平方和(sum of squre),包括:
残差平方和(Residual Sum of Squre, RSS)为827.378835,
总体平方和(Total Sum of Squre, TSS)为2443.45946,
以及估计平方和(Model Sum of Squre, MSS)为1616.08062
df 代表三种SS对应的自由度:
Residual Sum of Square对应的自由度为71 (TSS-MSS)
Total Sum of Square对应的自由度为73 (样本量-1)
Model Sum of Square对应的自由度为2 (有两个自变量)
MS 代表平均平方和,等于SS/df
上办部分的右边则报告了回归模型的描述性统计量,依此包括:
Number of Obs:观测值数量,这里是74
F(2,71):F统计量,F值为69.34;
Prob > F:F值是否统计显著对应的p值,此处为0.00000 (F统计量显著代表解释变量对被解释变量有解释能力)
R-square:R平方,为0.6614;代表解释变量的变化能够在多大程度上解释被解释变量的变化。R^2=\dfrac{MSS}{TSS}=1-\dfrac{RSS}{TSS} ,数值越大,代表模型拟合优度越高,自变量能够解释的比例越高。
Adj R-squre: 调整R平方,在R-squre的基础上调整自由度,避免过多自变量。Adj.\; R^2 = 1-\dfrac{(1-R^2)(n-1)}{(n-1-k)} ,可以看出,随着k(自变量数量)的增加,Adj.\; R^2 会减小。
Root MSE是root mean square error即均方误差,简写为RMSE,为3.4137,RMSE是平均残差平方和的平方根,即 RMSE=\sqrt{MSR}
下半部分则报告了回归系数相关的结果。第1列是变量名称,第2列是估计系数,第3列是系数对应的标准误,第4列是检验系数=0对应的t统计量,第5列是系数不=0的t检验的p值,第6列是估计系数95%的置信区间。
例如:weight变量的估计系数为-0.0038515,假设检验“系数(-.0038515)=0”的t-检验t值为-2.43,p值为0.018。注意,t值=估计系数(Coef.)/标准误(Std. Err.)
因此基于auto.dta数据,我们得到的mpg和weight,length变量之间的线性关系为:
mpg = -0.0038515\; weight+-0.0795935\; length+48.88487
在回归分析中,需要对模型的整体和系数进行显著性检验,以求证其是否符合经济理论或显示情况的要求。其实在结果中已经展示了最基本的F检验和t检验的结果:
在回归系数部分,默认展示了每个变量“估计系数=0”这一原假设的t-检验结果。例如在上面的例子中,我们可以得出结论,在95%的置信水平下,我们认为weigth变量的系数显著不等于0,常数项也显著不等于0,而length变量的系数在95%的知心水平下与0没有显著区别。
模型的预测
predict命令是regress命令的后续命令。(后续命令即postestimation,在help regress打开的帮助页面 Syntax 部分最后有提示: See [R] regress postestimation for features available after estimation. 通过点击或者直接 输入命令help regress_postestimation就会打开regress后续命令的窗口。可以看到除了predict命令之外,还有其他多种命令,可以根据需要后续自行学习。)
当使用regress命令完成因变量对自变量的回归,predict命令可以用来得到因变量的预测值(也称为拟合值)和残差。拟合值的计算是通过regress命令得到的估计系数 \boldsymbol{\beta} 和自变量 \boldsymbol{x} 相乘得到的取值,即 \hat{\boldsymbol{y}} = \boldsymbol{x} \boldsymbol{\hat{\beta}} ,而残差定义为因变量的实际值和预测值的差值:\boldsymbol{e} = \boldsymbol{y} - \hat{\boldsymbol{y}} 。
predict命令的格式如下:
predict [type ] newevar [if ] [in ] [,single_options]其中,predict是命令的名称,newvar代表保存预测值的新变量的名称。if和in和之前介绍的一致,分别是条件判断和范围判断。single_options是对应的选项,用于指定计算预测值还是残差。
仍然以8.2.1节中回归为例,我们考察变量weight 和length 对于mpg变量的影响。我们利用predict命令分别基于xb和residual 两个option分别得到预测值和残差。
sysuse auto, clear regress mpg weight length predict mpg_hat, xb predict e , residuallist mpg weight length mpg_hat e in 1/5
. sysuse auto, clear
(1978 automobile data)
. regress mpg weight length
Source | SS df MS Number of obs = 74
-------------+---------------------------------- F(2, 71) = 69.34
Model | 1616.08062 2 808.040312 Prob > F = 0.0000
Residual | 827.378835 71 11.653223 R-squared = 0.6614
-------------+---------------------------------- Adj R-squared = 0.6519
Total | 2443.45946 73 33.4720474 Root MSE = 3.4137
------------------------------------------------------------------------------
mpg | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
weight | -.0038515 .001586 -2.43 0.018 -.0070138 -.0006891
length | -.0795935 .0553577 -1.44 0.155 -.1899736 .0307867
_cons | 47.88487 6.08787 7.87 0.000 35.746 60.02374
------------------------------------------------------------------------------
. predict mpg_hat, xb
. predict e, residual
. list mpg weight length mpg_hat e in 1/5
+----------------------------------------------+
| mpg weight length mpg_hat e |
|----------------------------------------------|
1. | 22 2,930 186 21.79566 .2043426 |
2. | 17 3,350 173 21.21275 -4.212752 |
3. | 22 2,640 168 24.34527 -2.345268 |
4. | 20 3,250 196 19.76725 .2327502 |
5. | 15 4,080 222 14.50109 .4989072 |
+----------------------------------------------+
.
虚拟变量作为自变量的回归
虚拟变量是指取值只有0和1两种情况的变量。虚拟变量作为自变量与连续变量作为自变量下OLS回归的命令没有差别。但是其经济意义是大家需要了解的。
例如系统自带数据auto.dta中的foreign变量。当虚拟变量作为自变量出现在回归中,估计系数代表虚拟变量两个取值对应的两组数据之间因变量的差别。
例如在模型 mpg=\beta_0 + \beta_1 \; foreign 中,\beta_0 的含义是当变量 foreign=0 的情况下,mpg 变量的均值;\beta_1 的含义是进口车(foreign=1 )mpg的均值与本国车(foreign=0 )mpg均值的差值。
例如下面的代码就给出了foreigh,weight和length对mpg的影响
sysuse auto, clear reg mpg foreign reg mpg foreign weight length 第2个模型中foreign的估计系数的含义是,在保持变量 weight 和 length 不变的情况下,foreign=1 组内mpg的大小相对 foreign=0 组内mpg大小的平均差值,即边际效应。
B.基于某个变量取值的虚拟变量
上面例子中我们仅有一个虚拟变量,这是因为foreign仅有2个取值,换句话说,foreign变量的取值将整个样本分成了两个部分,而虚拟变量的估计系数代表了两个分组内因变量均值的差值。如果有多个分组,我们想要知道每个分组的因变量差异,这时可以引入多个虚拟变量来实现。
仍以auto.dta数据为例,假设我们要考察维修次数(rep78)、weight、lenghth对里程mpg的影响。rep78变量是汽车维修记录次数,该变量的74个观测值中有5个取值为缺失值,2个观测值取值为1,8个观测值取值为2,30个观测值为3,18个取值为4,11个取值为5。而且我们关注的是维修次数低于3次(即1次、2次)、维修次数等于3次和维修次数大于3次(即4次、5次)这三个分组之间的区别。
我们可以首先生成一个变量group(取值分别为1、2、3)代表着三个取值。然后借助tabulate命令生成三个虚拟变量d_group1、d_group2、d_group3,对应三种取值情况:
sysuse auto, clear gen group = . replace group = 1 if rep78 < 3 replace group = 2 if rep78 == 3replace group = 3 if rep78 > 3 & rep78 < . tab group , miss tab group tab group , generate (d_group)接下来可以通过如下回归模型考察三类汽车之间的价格差异:
regress price d_group1 regress price d_group1 d_group2 regress price d_group1 d_group2 d_group3 // 虚拟变量陷阱 regress price d_group1 d_group2 mpg headroom
将结果表格输出到word文档
在学术论文中,我们需要将诸如描述性统计结果、相关系数结果、单变量检验结果、以及回归结果等整理成表格。然后将表格放到诸如Word文档、Excel文档或者Latex文档中去。这些表格一般都是三线表的形式。
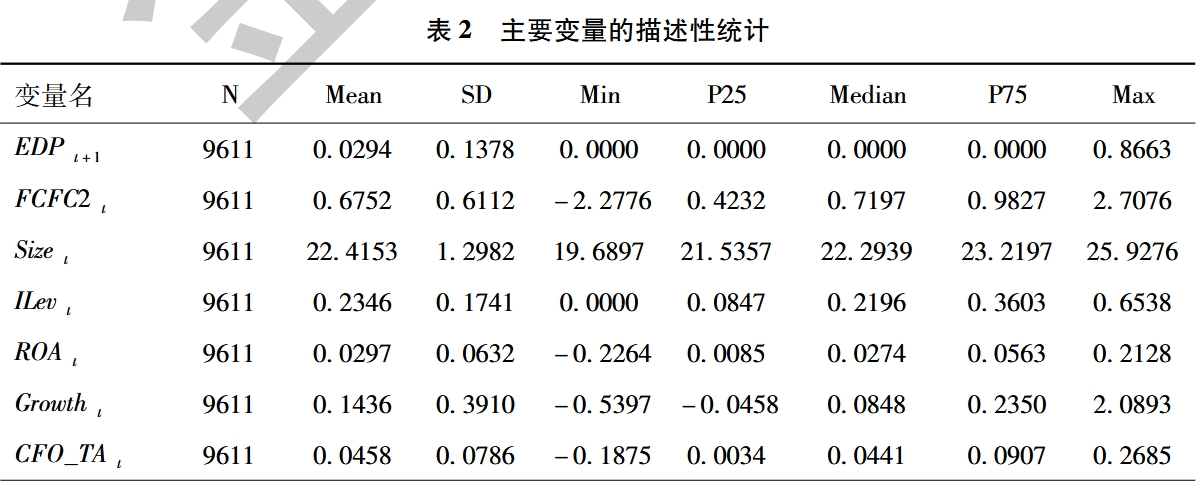
通常,在描述性统计表格中,每一行是一个变量的信息,每一列是一个我们关心的统计量,下面的截图来自于论文《自由现金流量创造力与违约风险——来自A股公司的经验证据》,我们在 章节 10
可以看到第一列是列名,后续依次是样本量(N)、均值(Mean)、标准差(SD)、最小值(Min)、25%分位数(P25)、中位数(Median)、75%分位数(P75)、最大值(Max)
尽管现在的期刊论文中大多省略了相关系数表格,但在工作论文阶段或者探索分析阶段,报告相关系数表格对于自己以及论文合作者判断结果是否正确仍然有很大的价值。
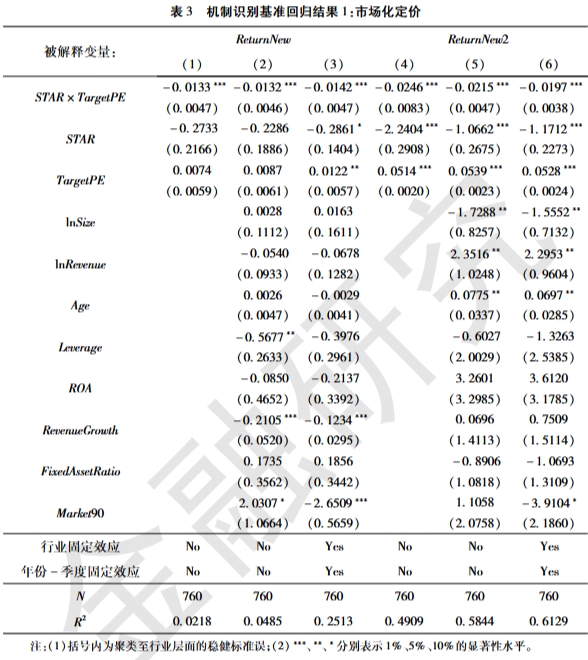
大量的实证表格都是与回归结果相关的,例如下面的截图展示了一个典型的回归结果表格,来自论文《科创板注册制如何提升IPO定价效率?——来自双重差分模型的因果识别证据》我们在 章节 10
你可以通过手动复制的方式,将结果拷贝的Excel/WPS/Word中去,但这样费时费力还容易出现错误。Stata的功能强大之一就是存在一些方便快捷的第三方命令,可以实现我们的功能。目前已经有了非常多第三方命令生成论文中基本可以直接使用的表格,本章我们将使用命令sum2docx生成描述性统计表,利用corr2docx命令生成相关系数表,利用t2docx生成t检验表格,利用reg2docx、esttab、outreg2命令生成回归结果表格。需要注意的是sum2docx、corr2docx、t2docx、reg2docx只能在Stata15以及更新的版本中使用,早期的版本可以借助其他的命令(可以自行网络检索查找)
这几个命令需要安装,可以使用ssc install完成安装:
ssc install sum2docx
ssc install corr2docx
ssc install t2docx
ssc install reg2docx完成安装之后,可以通过help命令查看对应的帮助文档了解命令的语法结构。
这两个命令曾经有过大的版本变动,如果直接去互联网上检索资料,可能得到的用法是基于旧版本的,其语法规则并不适用于当前安装的命令(我们上面的例子是基于最新版的语法举例),请务必通过 help sum2docx, helpl corr2docx查看命令对应的帮助文档,使用最新的语法,无论什么命令,请以help 手册中的信息为准 。
描述性统计表格输出
sysuse auto, clear /// using "C:/StataClass/chap_table/summary.docx" , replace /// stats (N mean (%9.2f) sd min (%9.0g) median (%9.0g) max (%9.0g)) /// title ("表 1: 描述性统计" ) /// note ("Data source: auto.dta" )
相关系数表格输出
sysuse auto, clear weight length rep78 foreign /// using "C:/StataClass/chap_table/correlation.docx" , replace /// star (* 0.1 ** 0.05 *** 0.01) /// title ("this is the coefficient of correlation" ) /// note ("* 0.1 ** 0.05 *** 0.01" )
t检验结果输出
sysuse auto,clear weight length mpg rep78 headroom trunk /// using "C:/StataClass/chap_table/t-test.docx" , replace /// by (foreign) star (* 0.1 ** 0.05 ** 0.01) /// title ("this is the t-test table" ) /// note ("Data source: auto.dta" )
回归结果输出
在学术期刊中,表格中的回归结果通常以竖向形式展示,每一列是一个回归模型,结果中通常需要展示:每一个变量的估计系数及其对应的t值(或者standard error,或者p值)、回归观测值数量、R-squre(或者 Adjusted R-square)。
我们可以使用esttab命令或者outreg2命令将回归结果按照期刊常见的格式输出到Excel或者Word文档中。esttab 和outreg2都是第三方命令。
esttab命令输出
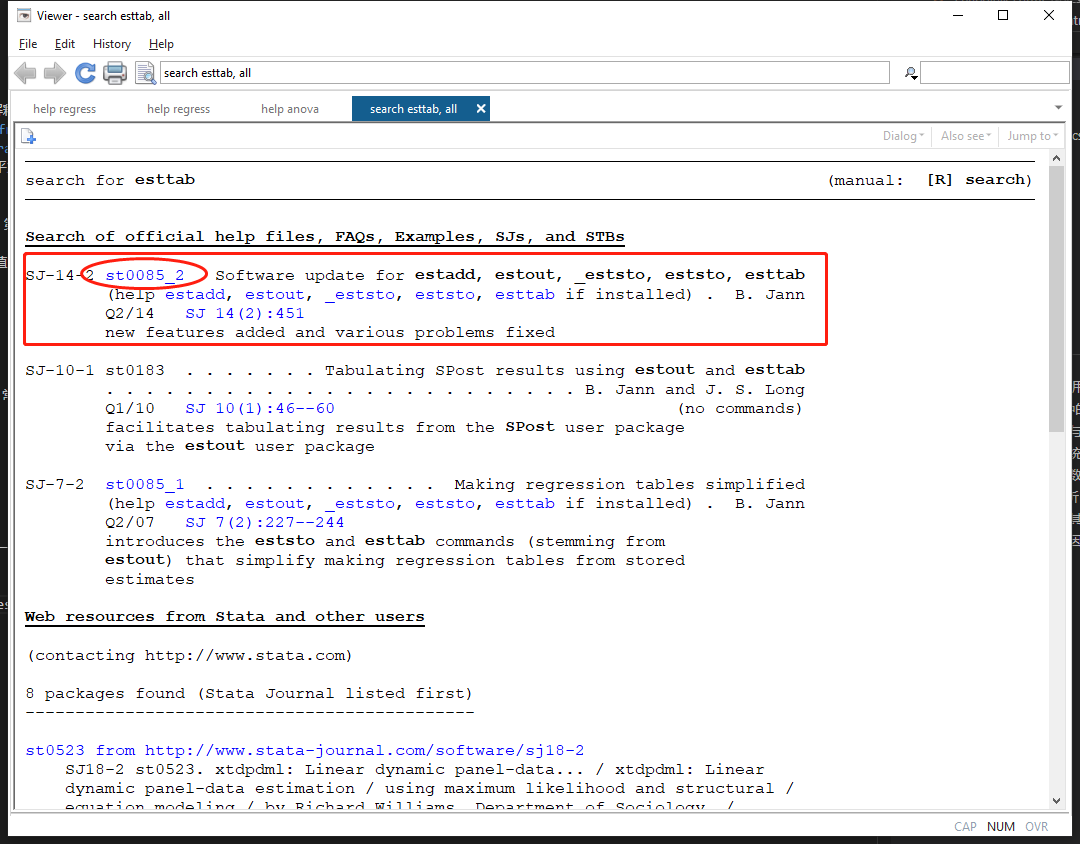
esttab命令通过findit esttab,在打开的搜索结果窗口中点击 “st0085_2”
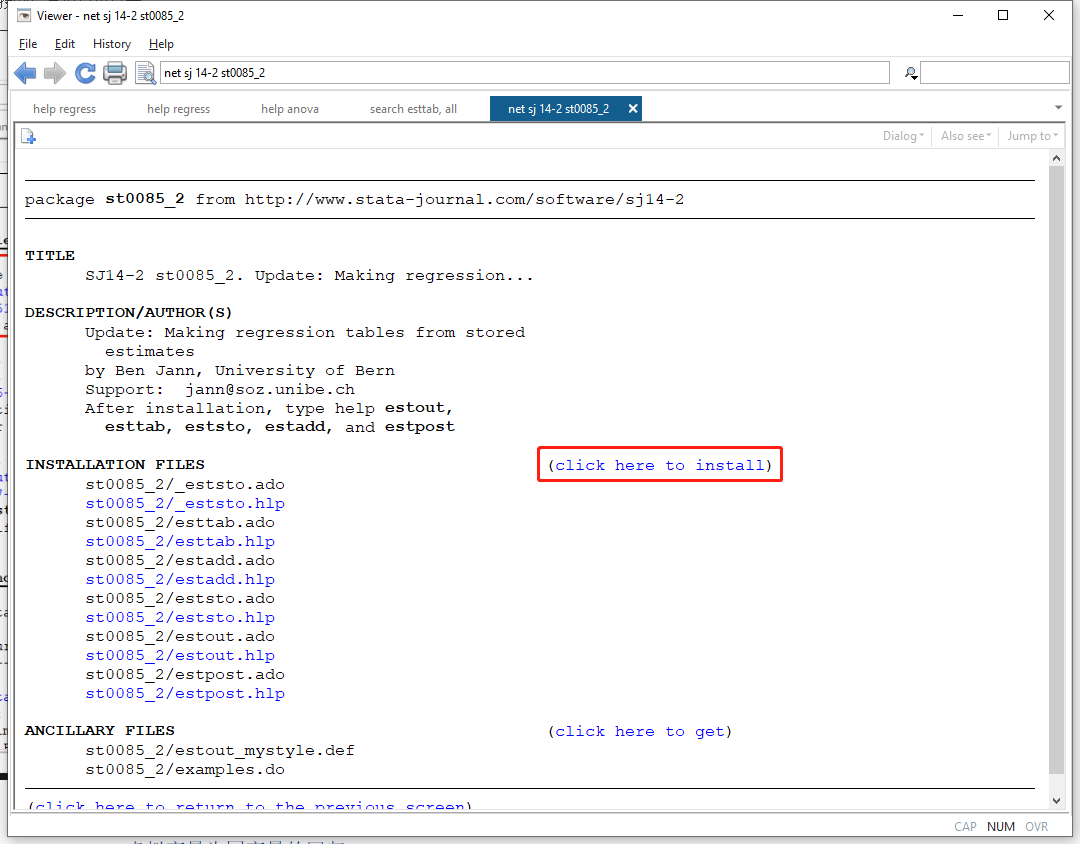
会弹出一个新的窗口,点击click here to install就可以安装该命令了
上述安装步骤等同于命令net install st0085_2.pkg, replace
安装成功后,可以通过help esttab打开帮助文档,还可以结合网页 http://repec.org/bocode/e/estout/hlp_estpost.html 学习。(当然你也可以找到很多中文的学习资料)
下方命令可以将三个回归结果分别输出到rtf文件。
global PATH "C:/StataClass/chap_table" sysuse auto, clear regress mpg weight estimates store ols1 reg mpg length estimates store ols2 reg mpg weight length estimates store ols3 using "${PATH}/01regression.doc" , replace rtf /// star (* 0.1 ** 0.05 *** 0.01) staraux compress /// order (length weight )上述代码将回归结果输出到C:/StataClass/chap_table目录下的01regression.doc文件中。
在这段代码中,estimates store ols1的功能是将这条命令之前的regression命令得到的回归结果存储到ols1中;类似的第2个回归、第3个回归分别被存放在了ols2, ols3中。
esttab ols* using "${PATH}/01regression.doc", replace rtf r2 staraux compress star(* 0.1 ** 0.05 *** 0.01)命令实现了结果的输出。各个部分的含义如下:
esttab ols*:输出的内容涵盖所有的以ols开头的结果(在我们这里就是ols1, ols2, ols3),等价于 esttab ols1 ols2 ols3using "${PATH}/01regression.doc":指定输出的文件,结合option rtf共同决定了输出的是rtf格式(word的通用格式)rtf:指定了输出文件的格式,rtf代表富文本格式可以使用word打开。这里rtf还可以换成其他值(参见esttab的帮助文档),例如常见的情况是可以改成csv(输出csv文件,可以用excel打开)或者tex(输出tex文件,用于latex表格)replace:如果输出文件已经存在,就用新文件替换。r2:输出R-square。当然也可以用ar2替换r2,这样输出的就是Adjusted R-square;或者在其他回归命令下需要输出Pesudo R-squre的时候,可以用pr2替换。star(* 0.1 ** 0.05 *** 0.01):设定显著性水平的符号,这里10%水平上显著用一颗星表示、5%的水平上显著用两颗星表示、1%的水平上显著用三颗星表示。如果在10%的水平上仍然统计不显著,不加任何符号。staraux:将表示显著性的星号放在t值而不是放在系数上。compress:将表格中的垂直距离压缩,是表格更加紧凑。order(length weight): 改变自变量的显示顺序,默认情况下,esttab命令会按照回归模型中每个变量出现的先后顺序安排自变量的顺序,越早出现的变量在输出的回归表格中越靠上,而越晚出现的变量则越靠下。我们可以使用order(varlist)来手动指定自变量的排列顺序。例如在本例中,weight变量出现更早(第一个回归就出现了),length变量出现更晚(第二个回归才出现),默认情况下输出结果中应该是weight变量排在上方,但我们通过 order(length weight)调整了显示顺序,让length变量排在了上方。
另外,需要指出的是如果是重复执行的情况,在已经打开了对应的word文件下,再次运行代码会有错误提示:file 01regression.doc is read-only; can not be modified or erased。
当然esttab还有其他更复杂的应用,请结合上文提到的estout网页或者esttab的帮助文档进一步学习。
outreg2命令输出
通过命令ssc install outreg2可以安装outreg2命令。可以增加一个replac的option即:ssc install outreg2, replace。
安装成功后,通过help outreg2即可通过帮助文档学习outreg2命令的用法。
下面的代码实现了和esttab例子中同样的功能:
sysuse auto, clear regress mpg weight using "${PATH}/01regression_outreg2.doc" , replace word excel /// reg mpg length using "${PATH}/01regression_outreg2.doc" , append word excel /// reg mpg weight length using "${PATH}/01regression_outreg2.doc" , append word excel /// esttab和outreg2两个命令都可以实现回归结果的输出,选择一个使用即可。
练习
1.利用数据auto.dta,熟悉regress命令和重要的option。完成如下任务:
a.将mpg作为因变量,headroom和gear_ratio作为自变量,完成OLS回归,并解释两个自变量的估计系数是否在95%的置信水平下统计显著?每个自变量估计系数的经济意义是什么?模型的拟合优度是多少?
b.在1的基础上,加入beta这一option并对比如下命令的结果,体会该option的作用
sysuse auto, clear foreach var of varlist mpg headroom gear_ratio {gen std_`var' = std (`var' ) reg std_mpg std_headroom std_gear_ratioreg mpg headroom gear_ratio, betac.完成如下3个回归模型,并分别使用esttab命令和outreg2命令将结果导出到word/excel文件(当然,如果是用esttab命令,本质上是输出的rtf格式和csv格式的文件)中
mpg = \alpha + \beta_1 weight + \varepsilon
mpg = \alpha + \beta_1 weight + \beta_2 length + \varepsilon
mpg = \alpha + \beta_1 weight + \beta_2 length + \beta_3 weight*length+ \varepsilon
其中 weight*length 是变量 weight 和变量 length 的乘积。